🌈 个人主页:(时光煮雨)
🔥 高质量专栏:vulnhub靶机渗透测试
👈 希望得到您的订阅和支持~
💡 创作高质量博文(平均质量分95+),分享更多关于网络安全、Python领域的优质内容!(希望得到您的关注~)
🌵目录🌵
- 难度 ⭐⭐⭐⭐⭐
- 题目回顾
- ✅解题思路分析
-
- 💖 概述
- 💓 核心思路
- ✅ 代码分析
- ✅ 复杂度分析
- ✅ 测试用例验证
-
- ✅ 示例1
- ✅ 示例2
- ✅ 示例3
- ✅ 边缘用例
- 💖 总结
- 🤝 期待与你共同进步
- 📚 参考文档
难度 ⭐⭐⭐⭐⭐
题目回顾
在一个 n x n 的整数矩阵 grid 中,每一个方格的值 grid[i][j] 表示位置 (i, j) 的平台高度。
当开始下雨时,在时间为 t 时,水池中的水位为 t 。你可以从一个平台游向四周相邻的任意一个平台,但是前提是此时水位必须同时淹没这两个平台。假定你可以瞬间移动无限距离,也就是默认在方格内部游动是不耗时的。当然,在你游泳的时候你必须待在坐标方格里面。
你从坐标方格的左上平台 (0,0) 出发。返回 你到达坐标方格的右下平台 (n-1, n-1) 所需的最少时间 。示例 1:
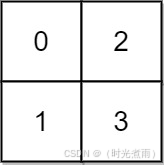
输入: grid = [[0,2],[1,3]]
输出: 3 解释: 时间为0时,你位于坐标方格的位置为 (0, 0)。
此时你不能游向任意方向,因为四个相邻方向平台的高度都大于当前时间为 0 时的水位。 等时间到达 3 时,你才可以游向平台 (1, 1).
因为此时的水位是 3,坐标方格中的平台没有比水位 3 更高的,所以你可以游向坐标方格中的任意位置示例 2:
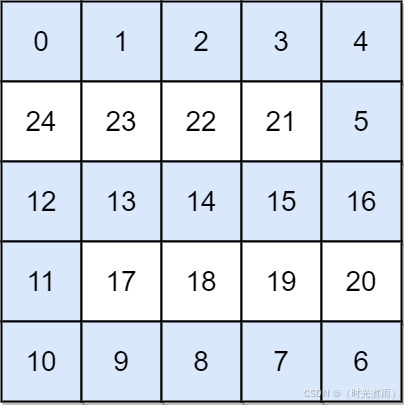
输入: grid = [[0,1,2,3,4],[24,23,22,21,5],[12,13,14,15,16],[11,17,18,19,20],[10,9,8,7,6]]
输出: 16
解释: 最终的路线用加粗进行了标记。 我们必须等到时间为 16,此时才能保证平台 (0, 0) 和 (4, 4) 是连通的提示:
- n == grid.length
- n == grid[i].length
- 1 <= n <= 50
- 0 <= grid[i][j] < n²
- grid[i][j] 中每个值 均无重复
✅解题思路分析
💖 概述
本题的目标是寻找从网格左上角 (0, 0)到右下角 (n-1, n-1)的最少时间,其中时间 t表示水位高度。在时间 t时,只能在水位淹没相邻平台时移动。我们需要找到一条路径,使得路径中所有平台高度的最大值最小化,这个最大值即为所需的最少时间。
💓 核心思路
- 问题转化:将游泳问题转化为寻找一条从起点到终点的路径,使得路径上的最大高度最小。
- Dijkstra 算法变种:使用优先队列(最小堆)实现,每次扩展当前水位最低的路径。
- 贪心策略:总是优先处理当前水位最低的节点,确保在尽可能低的水位下扩展路径。
- 关键点:路径所需时间由路径中所有平台高度的最大值决定,而非路径长度。
✅ 代码实现
1import heapq 2from typing import List 3 4 5class Solution: 6 def swimInWater(self, grid: List[List[int]]) -> int: 7 # 初始化:res记录路径中的最大高度(即所需时间),n为网格尺寸 8 res = 0 9 n = len(grid) 10 11 # 使用最小堆存储(高度,x坐标,y坐标),初始点为左上角(0,0) 12 heap = [(grid[0]
《【LeetCode - 每日1题】水位上升的泳池中游泳问题》 是转载文章,点击查看原文。